The quest to understand time has driven humanity for millennia, evolving through philosophy, classical mechanics, and quantum theory. The concept of fundamental time, a minimal unit of time, reflects this journey, filled with insights and mysteries.
In my previous article, Planck Scale Pioneers (Part 1): Max Planck, Planck Units, and the Quantum Revolution, we explored Max Planck’s contributions to establishing the Planck scale. Planck’s introduction of quantized energy levels and his fundamental constant would bridge quantum mechanics and relativity. Continuing this journey in Part 2, we delve into the concept of fundamental time and its historical development. In the early 20th century, Poincaré introduced the idea of quantum discontinuity, suggesting a fundamental time interval. This idea positioned Poincaré at the critical juncture between classical and quantum physics.
One fascinating aspect of fundamental time is its scale. To appreciate this, consider: In the time it takes to snap your fingers, more Planck time units have elapsed than there have been seconds since the Big Bang. Planck time, approximately 5.39×10⁻⁴⁴ seconds, is unimaginably small, highlighting the limitations of our current physical theories. Resolving this timescale is beyond today’s technological capabilities. However, just as Brownian motion provided indirect evidence of atoms, we hope to uncover indirect signatures of physics near the Planck scale. While we cannot directly measure Planck time, its effects might be observable through innovative experiments and theoretical models.
Max Planck’s introduction of the Planck constant in 1900 suggested a fundamental unit of action, hinting at a minimal time scale. Albert Einstein’s theory of special relativity transformed our understanding of time, yet it was Henri Poincaré who, in the early 20th century, explicitly linked the concept of a fundamental time unit to the emerging quantum theory. His work on quantum discontinuity around 1911–1912 laid crucial groundwork for our modern conception of spacetime at its most fundamental level.
The Concept of Fundamental Time: Historical Development
The idea of indivisible time units dates back to ancient Greek philosophy. Around 450 BCE, Zeno of Elea hinted at this through his paradoxes on infinite divisibility. Centuries later, scholars like Nicholas of Cusa also speculated about indivisible units of time and space.
In the modern era, Isaac Newton introduced the concept of absolute time — a universal flow unaffected by external factors. While not proposing a fundamental time unit, Newton’s work set the stage for later debates about the nature of time. Leibniz, argued for a relational view of time, positing that time only exists in relation to events and objects. This philosophical divide influenced science for centuries.
By the 19th century, thinkers like Ernst Mach began to critically question absolute time. Mach’s focus on observable phenomena influenced Einstein and other pioneers of modern physics.
The early 20th century brought new perspectives on time. Max Planck’s introduction of the Planck constant in 1900 suggested a fundamental unit of action, affecting our understanding of time at the smallest scales. Albert Einstein’s theory of special relativity in 1905 linked time with space, showing its relative nature. Around 1911–1912, in his final research push, Poincaré proposed quantum discontinuity, including the possibility of a fundamental time unit, explicitly connecting this idea to quantum theory and spacetime.
In the 1950s and 1960s, physicists began exploring the implications of combining quantum mechanics with general relativity, leading to new insights into the nature of time and space. In 1964, C. Alden Mead proposed a fundamental length, hinting at a fundamental time unit as well. By 1978, developments in quantum gravity, informed by the work of physicists like Abdus Salam, helped solidify the understanding of Planck time as a key concept. This provided a clearer framework for understanding the smallest possible intervals of time, building on the foundational ideas introduced by Max Planck.
The Concept of Planck Time: Development and Implications
Planck time represents the smallest meaningful time interval. It emerged as physicists sought to reconcile quantum mechanics with general relativity. The concept highlights the limits of our current physical theories, where time and space become discrete at the quantum level.
At its core, Planck time (tₚ) is defined by a seemingly simple expression:
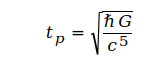
This elegant formula combines three of the most fundamental constants in physics: the reduced Planck constant (ℏ) introduced by Dirac and remember me the expression In Hoc Signo Vinces, which is central to quantum mechanics; the gravitational constant (G), which governs the strength of gravity; and the speed of light in vacuum c, from special relativity.
When we plug in the values for these constants, we arrive the very small number: approximately 5.39 × 10⁻⁴⁴ seconds.
To understand where we stand in probing the Planck scale, recent advancements in atomic clock technology have set new records in time measurement precision. A July 2024 study by Aeppli, Kim, Warfield, Safronova, and Ye, published in Physical Review Letters, reported a clock with a systematic uncertainty of 8×10⁻¹⁹. This marks a significant leap in our ability to measure time with extreme accuracy, edging us “closer,” though not yet “closer to the truth,” in probing the fundamental nature of time. While still many orders of magnitude away from directly measuring Planck time, these ultra-precise clocks open up new possibilities for testing new physics.
Poincaré’s Innovative Approaches to Quantum Theory and Time
on quantum theory introduced new ideas about the interaction between matter and radiation. He used Fourier analysis and statistical mechanics to propose quantum discontinuities, implying a granular conception of time.
One of Poincaré’s key ideas was his model of short-period resonators interacting with long-period resonators. This model provided a new way to conceptualize the interaction between matter and radiation at the quantum level by focusing on the partition of energy within this system. The equipartition theorem on statistical mechanics, states that energy is shared equally among all accessible degrees of freedom in a system at thermal equilibrium. Poincaré’s proofs offered new ways to understand this concept. His model of interacting resonators implies that energy exchanges, and thus time evolution in quantum systems, occur in discrete steps rather than continuously.
Poincaré’s development of an “inverse statistical mechanical theory” was also pioneering. This approach allowed physicists to infer microscopic behavior from macroscopic observations, inverting the traditional approach of statistical mechanics.
The full mathematical justification for Poincaré’s intuitions about discontinuities would come years later. In 1926, Paul Dirac introduced the delta function for use in quantum physics. This mathematical tool provided a rigorous way to represent instantaneous events or point-like objects, precisely the kind of discontinuities Poincaré had postulated. The Dirac delta function, while not considered a well-defined mathematical entity until 1945, offered a formal representation of the quantum discontinuities that Poincaré had identified. This development fully justified Poincaré’s use of Fourier methods in his inverse statistical mechanical theory, bridging the gap between his physical insights and the mathematical formalism of quantum mechanics.
Poincaré’s work on quantum theory, though over a century old, still holds relevance in modern physics. It provides historical context for the development of quantum mechanics and offers innovative approaches that can inform current research. As we continue to explore the nature of time in quantum mechanics and work to reconcile it with general relativity, Poincaré’s insights remain a valuable resource, showcasing the lasting impact of creative, interdisciplinary thinking in physics.
Love and Reason!